Using tree diagrams to organise notes.

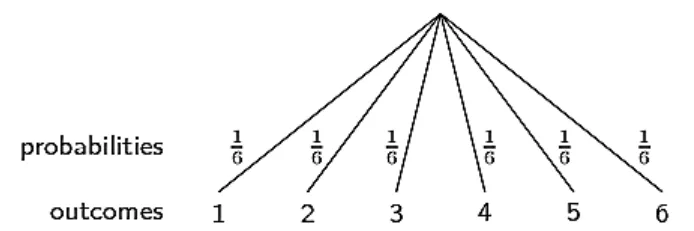
 Tree diagrams are useful for organising and visualising the different possible outcomes of a sequence of events. For each possible outcome of the first event, we draw a line where we write down the probability of that outcome and the state of the world if that outcome happened. Then, for each possible outcome of the second event we do the same thing.

Note that each outcome (the numbers 11 to 66) is shown at the end of a line; and that the probability of each outcome (all 1616 in this case) is shown shown on a line. The probabilities have to add up to 11 in order to cover all of the possible outcomes. In the examples below, we will see how to draw tree diagrams with multiple events and how to compute probabilities using the diagrams.

Earlier in this chapter you learned about dependent and independent events. Tree diagrams are very helpful for analysing dependent events. A tree diagram allows you to show how each possible outcome of one event affects the probabilities of the other events.

Tree diagrams are not so useful for independent events since we can just multiply the probabilities of separate events to get the probability of the combined event. Remember that for independent events:

P(A ans B) = P(A) X P(B)

So if you already know that events are independent, it is usually easier to solve a problem without using tree diagrams. But if you are uncertain about whether events are independent or if you know that they are not, you should use a tree diagram.

Subcribe on Youtube - IGNOU SERVICE

For PDF copy of Solved Assignment

WhatsApp Us - 9113311883(Paid)